やさしく解説!一般の人にはとっつきにくい「デシベル(dB)表示」
オーディオの世界に関わらすエンジニアの世界では、デシベル(dB)表示が非常によく使用されます。
このデシベル(dB)表示、本当にとっても便利なのですよ。だから、エンジニアはデシベル(dB)表示が大好きなのです。この記事を書いている私も、「ボリュームを6dB増やす」とかよく使います。
でも一般の人にはなじみの無いデシベル(dB)表示。小学生や中学生の理科では全く学習しませんし、家電のカタログにはよく出てくるのに、「何のこっちゃ?」って感じですよね。そこで、今回はこのよく知らないのによく目にするデシベル(dB)表示について説明したいと思います。
デシベル表示は相対値です。絶対値ではありません。
まずdBは何を現しているかというと、何かの数値に対して「何倍」だとか「何分の1」だとかを表しています。
例えば「音量が6dB増えた」と「音量が2倍に増えた」は同じ意味になります。
よくあるデシベル(dB)表示の間違えた使い方として、絶対値のような表現にしてしまうというのがあります。
色々なカタログを見ても、XXXの項目の仕様はXXdBとか書いてあるので絶対値であると思われがちですが、デシベル(dB)は必ず相対値を表すときに使用します。
ちなみに、相対値と絶対値について補足すると。。。
「体重がXXkgです」は絶対値。XXkgは誰がどう見てもXXkgであり全世界共通です。
「Aさんの体重はBさんの2倍だ」は相対値を使用した表現になります。何故なら比較対象のBさんの体重がわからないとAさんの体重がわからないからです。
「Aさんの体重はBさんの2倍だ」はデシベル(dB)表示にすると「Aさんの体重はBさんと比べて6dBだ」となります。
ですので、「ボリュームの値がXXdBだ」は間違えた表現なのです。
これだけですと何と比べてボリュームがXXdBになったのかが解りません。
dBには必ず比較対象となるものが必ず必要なのです。
(カタログに書かれたデシベル(dB)表示は大抵暗黙のうちに比較となる基準が決められています。でもその比較対象はどこにも記載されていないことが多いのです)
具体的なdBの計算方法
dBは20log(X倍)で表されます。(電力などについては10log(X)で表現されますが、ここでは電圧などに使用される20log(X)で統一します)これでは如何にも教科書的なのでWindowsOSに付いている関数電卓を使って具体的な計算をしてみます。
何倍をdB表示に変換する
計算例)
10倍は何dBでしょうか? 式だとdB = 20log(10倍)です。
1.10倍の10を入力します。
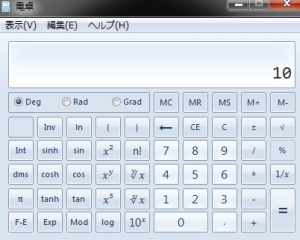
2.logボタンを押します
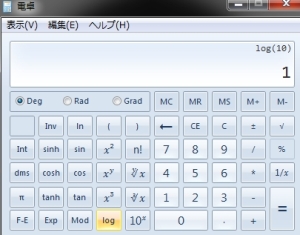
3.20を掛けます。
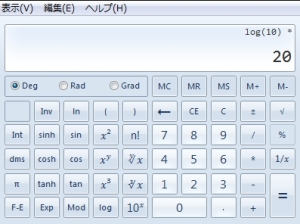
すると答えは20dBとなります。
上記と同様の計算をすると
2倍は約6dB
4倍は約12dB
1000倍は60dB
10000倍は80dB
100000倍は100dBとなります。
毎回電卓を使用するのも面倒なのでここに何倍⇒dBの変換ツール(java script)を置いておきます。
ちなみに+6dBは2倍なのですが、-6dBは1/2(0.5倍)の意味になります。
dB表示は前に付く符号により、「何倍」か「何分の1」かを表現します。
ここまで理解できるともっと複雑な倍数のdB表示が暗算で出来るようになります。
問題)128倍は何dBでしょうか?暗算で求めてみましょう。
答え)
128は4×4×4×2に分解できます。
2倍は6dB、4倍は12dBですから、
128倍は12dB(4倍)+12dB(4倍)+12dB(4倍)+6dB(2倍)と表すことができ、すべて足すと128倍は42dBであることがわかります。
問題)1600倍は何dBでしょうか?暗算で求めてみましょう。
答え)
3200は100×4×4×2に分解できます。
2倍は6dB、4倍は12dB、100倍は40dBですから、
3200倍は40dB(100倍)+12dB(4倍)+12dB(4倍)+6dB(2倍)と表すことができ、すべて足すと3200倍は70dBであることがわかります。
dB表示から何倍に変換する
今度はdBから何倍に変換してみましょう。
まずは関数電卓を使用した場合です。式は、何倍=10^(dB/20)となります。
計算例)
24dBは何倍でしょうか?
1.24(dB)÷20を計算します。
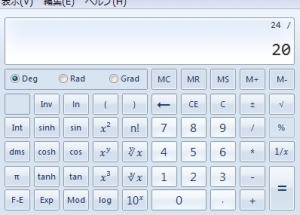
2.10^Xボタンを押します
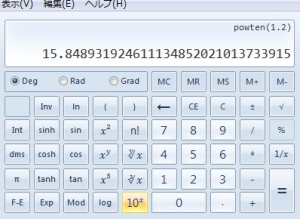
答えは約16倍となります。
毎回電卓を使用するのも面倒なのでここにdB⇒何倍の変換ツール(java script)を置いておきます。
こちらも暗算で簡単に変換できます。
例)42dBは何倍でしょうか?
答え)
42(dB)は12(dB)+12(dB)+12(dB)+6(dB)に分解できます。
6dBは2倍、12dBは4倍ですから
4倍×4倍×4倍×2倍と表現でき、42dBは128倍であることがわかります。
どうしてデシベル表示が使用されるのか
まず非常に大きな数字が少ない桁数の数字で表現できるので便利です。
100000倍を表現するときも100dBとたったの3桁で済みます。
それより便利なのは幅の広い数値をグラフで表現したときです。
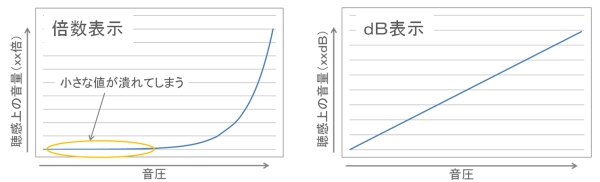
上記グラフは同じ内容のものをdB表示と倍数表示で示しています。
見て頂くとわかる通り、非常に大きな幅をもった数を表すとき、倍数表示だと小さな値がつぶれてしまいわからなくなってしまいます。その点、dB表示では細かな値のところまで表現することが可能です。
そもそも音の場合、取り扱う数値の幅が非常に大きく0(0dB)~100000(100dB)くらいの値を使用します。
このことからdB表示での扱いに適している分野なのです。
DAコンバーターとSNRの関係もdB表示が解れば理解できる
オーディオ好きの間ではUSB-DACが話題となっていますが、DAコンバーターというシステムを使用する以上物理的な性能限界があります。これはどんなに回路側の設計を頑張っても超えることのできない壁です。
DAコンバーターのSNRを例にとって性能限界について考えてみましょう。ちなみにSNRは(Signal-Noise Ratio)で本来の信号とノイズとの比を表しています。SNRが大きいほど信号に対するノイズが少ないということになります。
まずは、例として4ビットのDACを見てみましょう。すべて音は4ビット(16通り)のデータに丸め込まれます。どんなに表現豊かな繊細な音も16通りにしか表現することができないのです。16段階からかずれた音は簡単に言えば四捨五入されるイメージです。ですので、基準の音の振幅を1とした場合、階段上にない中途半場な音が、階段上にたどり着くまでの距離(ノイズの大きさ)は下図から1/16(階段1段分)となります。この本来の場所から階段上に移動するノイズを量子化ノイズといいます。
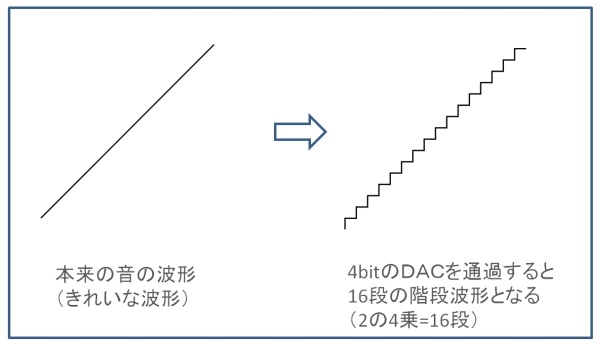
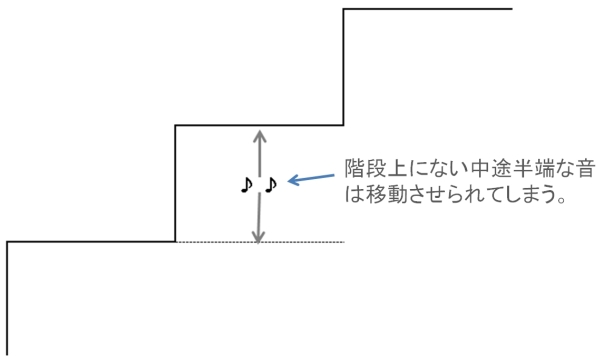
16段の階段上に無い中途半端な音はDACの中で無理やり一つ上の階段か一つ下の階段に移動させられる。この移動したときの距離がノイズとなる。このことからビット数の多いDACほど階段1段分の差が少なくなりノイズが少ない。よってSNRも良好。
信号に対して1/16(階段1段分)がノイズとなるので、SNRは次のように求めることができます。
Signal = 1
Noise = 1/16(階段1段分)
SNR= 1÷(1/16) = 16倍
この16倍をdBに変換すると24dBとなります。
※これは簡易的なSNRの求め方であり厳密な計算はもう少し複雑です。
同様の考え方をすると
5bitのDACでSNR=30dB
6bitのDACでSNR=36dBです。
このことからNビットのDACのSNRは
SNR(Nbit)=6dB x N(bit)となります。
ですのでCD音質16ビットの場合はSNRが6dB ×16bit = 約96dB。
ハイレゾ音源24ビットの場合はSNRが約144dBとなります。
上記で覚えた計算を使用すると、CDの場合96dB=約100000倍ですから、音楽の最大音量に対してノイズは100000分の1しかないことになります。これを考えるとCDはかなり音が良いことになります。
この16bit-DACの96dBというレベル。この程度ならまだよいのですが、DACの性能が20bitや24bitとなってくると本当にその性能がDACにあるのか測定するだけでも一苦労です。正直、かなりキチントした測定環境を整えないと高性能なDACの測定をすることは困難です。
例えば、シールドされた測定環境の中にある配線が風で揺れただけで測定値が変わってしまいます。(音響ノイズといって配線が揺れたことで配線間のカップリング容量が変化し、ノイズとして現れる)そのくらいシビアなのです。
そういった意味でいうと人間の耳はかなり高性能な測定器とも言えます。ちょっとした音の違いも、わかる人にはわかります。更に測定器では通常、音のスペクトルに対いて、SNRやTHDなど決められた内容を画一的に評価しますが、人の耳はその音の心地よさなどメンタルな部分も合わせて評価をします。SNRやTHDが良いから良い音だなんて決して評価をしません。真空管の音が良いなんていうのは最たるものです。Hi-Fiの音が素晴らしいということであれば、真空管の音なんて聞く人は居なくなっているのでしょう。
エンジニアは設計した機器の音響性能が1dB改善されることを目標に日々努力しています。それとは対照的に、音を音響性能に囚われず感性で評価しようとする人が沢山います。音は性能面とメンタル面の両方の見方で見ることができる数少ない分野です。だからこそ音楽は面白いのだと私は思います。


